Algoritmos de ordenação - O famoso Bubble Sort

O algoritmo
Uma implementação clássica, marcante e simples de ordenação de vetores, onde a cada iteração um elemento flutua para o topo. Humm! Dai vem o nome "Bolhas". Este é um assunto obrigatório em universidades ou cursos de programação.
Mesmo que grande parte dos nossos problemas sejam os frameworks e linguagens que escolhemos ter em nossas vidas, o estudo de algoritmo é essencial para desenvolvedores em geral, através desta dedicação, aprendemos técnicas que tornam nosso trabalho eficiente.

A implementação
Abaixo temos uma implementação do BubbleSort flexível que possibilita a ordenação crescente ou decrescente através do argumento (asc), a função privada __should_swap__ foi definida para a classificação dos valores, decidindo a troca de posições no vetor.
O array.copy foi utilizado para evitar um efeito colateral (side-effect) no argumento vetor.
def bubble_sort(array, asc=True):
output = array.copy()
size = len(output)
while size > 0:
new_size = 0
for current in range(1, size):
prev = current - 1
if __should_swap__(output, prev, current, asc):
swap = output[prev]
output[prev] = output[current]
output[current] = swap
new_size = current
size = new_size
return output
def __should_swap__(array, prev, current, asc):
if asc:
return array[current] < array[prev]
else:
return array[current] > array[prev]
def test_sort_asc():
numbers = [5, 4, 2, 1, 3]
result = bubble_sort(numbers, asc=True)
assert numbers == [5, 4, 2, 1, 3]
assert result == [1, 2, 3, 4, 5]
def test_bubble_sort_desc():
numbers = [4, 5, 2, 1, 3]
result = bubble_sort(numbers, asc=False)
assert numbers == [4, 5, 2, 1, 3]
assert result == [5, 4, 3, 2, 1]
Para validar o algoritmo use o pytest informando o nome do arquivo.
pytest -rA bubble-sort.pyTeste de mesa
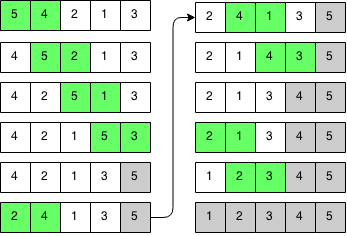
Os números da direita com menor valor são movidos (ou flutuados) para esquerda, quando classificamos como ordem crescente.
Qual o problema do BubbleSort?
No melhor cenário, o algoritmo retorna n de operações, onde n é igual ao tamanho do vetor, porém no pior cenário ele pode retornar n². O tamanho da lista irá determinar o tempo de processamento.
Para resolver estre problema existem diversos algoritmos para ordenação, com abordagens simples e sofisticadas:
Simples
Sofisticados
Finalizando
Este foi mais um exemplo de implementação de algoritmos, para relembrar ou adicionar ao seu kernel, até a próxima.
Time for feedback!